图像处理

简单的图像形成模型

当用数学方法描述图像信息时，通常着重考虑它的点的性质。例如一副图像可以被看作是空间各个坐标点的结合。它的最普通的数学表达式为：

$I=f(x,y,z,\lambda,t)$

其中，$(x,y,z)$是空间坐标，$\lambda$是波长，$t$是时间，$I$是图像强度。这样一个表达式可以代表一副活动的、彩色的、立体的图像。

当研究的是静止图像时，上式与时间$t$无关；当研究的是单色图像时，显然与波长$\lambda$无关；对于平面图像则与坐标$z$无关。因此，对于静止的、平面的、单色的图像来说其数学表达式可简化为：

$I=f(x,y),0<f(x,y)<\infty$

人们所感受到的图像一般都是由物体反射的光组成。函数$f(x,y)$可由两个分量来表示：

入射到观察场景的光源总量$i(x,y)$
场景中物体反射光的总量$r(x,y)$

$I=f(x,y)=i(x,y)r(x,y),0<i(x,y)<\infty,0<r(x,y)<1$

$i(x,y)$的性质取决于照射源，而$r(x,y)$取决于成像物体的特性。反射分量$r(x,y)$限制在0（全吸收）和1（全反射）之间。

$i(x,y)$的某些典型值：在晴朗的白天，太阳在地球表面产生的照度超过90000lm/m2。在有云的情况下，这个数值下降到1000lm/m2。在晴朗的夜晚，满月情况下大约为0.1lm/m2的照度。

$r(x,y)$的某些典型值：黑天鹅绒为0.01，不锈钢为0.65，白色墙为0.80。

Intrinsic image decomposition 本征图像分解

图像的数字化

大多数传感器的输出是连续电影波形。为了产生一副数字图像，需要把连续的感知数据转换为数字形式。所谓的图像数字化是指将模拟图像经过离散化之后，得到用数字表示的图像。

取样：

将在空间上连续分布的图像转换成离散的取样点（即像素）集的操作。由于图像是二维分布的信息，所以取样是在x轴和y轴两个方向上进行。

取样时注意：取样间隔的选取。取样间隔取得不合适除了画面出现马赛克之外，还会发生频率的混合现象。
量化：

将各个像素所含的明暗信息离散化后用数字来表示，称为图像的量化。一般的量化值用整数表示。充分考虑到人眼的识别能力后，目前非特殊用途的图像均为8 bit量化，即用0～255描述“黑～白”。

空间和灰度级分辨率

取样值是决定一副图像空间分辨率的主要参数，空间分辨率是图像中可辨别的最新细节。

在取样时，若横向的像素数（列数）为M ，纵向的像素数（行数）为N，则图像总像素数为 M * N 个像素。一般来说，采样间隔越大，所得图像像素数越少，空间分辨率低，质量差，严重时出现马赛克效应；采样间隔越小，所得图像像素数越多，空间分辨率高，图像质量好，但数据量大。

灰度级分辨率是指在灰度级别中可分辨的最小变化，由于硬件方面的要求，灰度级数通常是2的整数幂。

量化等级越多，所得图像层次越丰富，灰度分辨率高，图像质量好，但数据量大
量化等级越少，会出现假轮廓现象，图像质量变差，但数据量小

像素之间的邻域关系

4邻域：

像素$p(x,y)$的4邻域是$(x+1,y),(x-1,y),(x,y+1),(x,y-1)$
用$N_4(p)$表示像素p的4邻域

D邻域：

像素$p(x,y)$的D邻域是对角上的点$(x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1)$
用$N_D(p)$表示像素p的D邻域

8邻域：

$N_8(p)=N_4(p)+N_D(p)$

图像的放大与缩小

最近邻

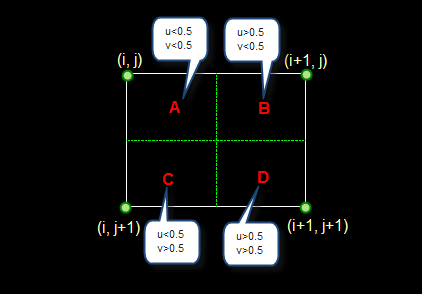
设i+u, j+v(i, j为正整数， u, v为大于零小于1的小数，下同)为待求像素坐标，则待求像素灰度的值 f(i+u, j+v)。

如果(i+u, j+v)落在A区，即u<0.5, v<0.5，则将左上角像素的灰度值赋给待求像素，同理，落在B区则赋予右上角的像素灰度值，落在C区则赋予左下角像素的灰度值，落在D区则赋予右下角像素的灰度值。

最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。
双线性插值

简明版

彩色图像表示

光学原理解释色彩的形成：

可视光区的波长在400nm~780nm，当光谱采样限制到三个人类视觉系统敏感的红、绿、蓝光波段时，对这三个光谱带的光能量进行采样，就可以得到一副彩色图像。

彩色视觉是人眼对射入的可见光光谱的强弱及波长成分的一种感觉。

彩色模型

颜色的描述是通过建立彩色模型来实现的，不同的彩色模型对应于不同的处理目的。

各种不同的颜色模型之间可以通过数学方法转换。

CIE(国际照明委员会)在进行大量的色彩测试实验的基础上提出了一系列的颜色模型：

RGB模型：红、绿、蓝三基色混合
HSI模型：色度(H, Hue)、饱和度(S, Saturation)、亮度(I, Intensity)

HSI彩色模型比较适合于人用色调、饱和度、亮度描述被观察物体颜色的解释，对于开发基于彩色描述的图像处理方法是一个理性的工具。
- H表示色调，用角度表示。 反映了该颜色最接近什么样的光谱波长。 0度为红色，逆时针120度为绿色，顺时针120度为蓝色。
- S表示饱和度，饱和度参数是色环的原点到彩色点的半径长度。在环的外围圆周是纯的或饱和的颜色，其饱和度值为1。在中心是中性（灰）色，即饱和度为0。
- I表示光照强度或亮度，它确定了像素的整体亮度，而不管其颜色是什么。
YUV模型：亮度(Y)、色度(UV)
YCbCr模型：亮度(Y)、色度(CbCr)

CMYK色系：用于印刷行业，是一种减色系统，将从白光中滤出三种原色之后获得的颜色作为表色系的三原色CMY

C (cyan)：青色/蓝绿色，从白色中滤去红色。

M (magenta)：品红，从白色中滤去绿色。

Y (yellow)：黄色，从白色中滤去蓝色。

彩色图像转变为灰度图像的处理称为彩色图像的灰度化处理。方法主要包括：最大值法、平均值法、加权平均值法。

最大值法：将输入图像中的每个像素的R、G、B分量值的最大者赋给输出图像中对应像素的R、G、B分量的方法。用公式可表示为：

$g_R(x,y)=g_G(x,y)=g_B(x,y)=max(f_R(x,y),f_G(x,y),f_B(x,y))$
平均值法：将输入图像中的每个像素的R、G、B分量的算术平均值赋给输出图像中对应像素的R、G、B分量的方法。用公式可表示为：

$g_R(x,y)=g_G(x,y)=g_B(x,y)=(f_R(x,y)+f_G(x,y)+f_B(x,y))/3$
加权平均值法：人眼对绿光的亮度感觉仅次于白光，是三基色中最亮的，红光次之，蓝光最低。相关研究表明，当$\omega_G$=0.587、$\omega_R$=0.299、$\omega_B$=0.114时，得到的灰度化图像较合理，此时灰度化公式就变为：

$g_R(x,y)=g_G(x,y)=g_B(x,y)=0.299\cdot f_R(x,y)+0.587\cdot f_G(x,y)+0.114\cdot f_B(x,y)$

第三章空间域图像增强

背景知识

基本灰度变换

直方图处理

空间滤波基础

平滑空间滤波器

锐化空间滤波器

混合空间增强法

图像增强：

突出图像中的某些信息，同时削去不需要的信息。

图像在传输或处理过程中会引入噪声或使图像变得模糊，从而降低了图像质量，甚至淹没了特征，给分析带来了困难。

白噪声，使得图看上去不清晰。

https://www.zhihu.com/question/47681952

空间域处理：点处理（图像灰度变换、直方图均衡）；邻域处理（线性、非线性平衡和锐化）

频域处理：高、低通滤波、同态滤波

https://blog.csdn.net/whuhan2013/article/details/53843974

空间域增强是指增强构成图像的元素，定义为：

$g(x,y)=T[f(x,y)]$

$f(x,y)$是输入图像

$g(x,y)$是输出图像

$T$是对$f$的一种操作，定义在$(x,y)$的邻域上

邻域：中心在$(x,y)$的正方形或矩形子图像

子图像中心从一个像素向另一个像素移动

基本灰度变换模型

灰度级变换函数：s=T(r)

T是一个1*1的矩阵，因此是点处理

三种基本类型：

线性的（正比或反比）
对数的（对数或反对数的）
幂次的（n次幂和n次方根变换）

图像反转：$s=L-1-r$

对数变换：$s=clog(1+r)$

幂次变换：$s=cr^{\gamma}$

反转变换：

适于处理增强嵌入于图像暗色区域的白色或灰色细节，特别是当黑色面积占主导地位时。

生成灰度反转图像。

对数变换：

使一窄带低灰度输入图像映射为一宽带输出值

可以用于扩展图像中的暗像素

（可以在某个区间内将输出灰度值拉伸很快，将原本黑色的区域拉伸到右图的效果。傅立叶变换图的对数变换处理）

幂次变换：

幂次曲线中的$\gamma$值决定了是否把输入窄带暗值映射到宽带输出值还是把输入窄带亮值映射到宽带输出。

应用：$\gamma$校正

用幂次变换进行对比度增强

分段线性变换：

对比拉伸：扩展图像处理时灰度级的动态范围

起点：

终点：

线性函数：

阈值函数：

对比拉伸：
灰度切割：提高特定灰度范围的亮度

（相当于做了一个范围内的二值化处理）
位图切割：把数字图像分解成位平面（每一个位平面可以处理成一幅二值图像，即要么是0要么是255）

高阶位如前4位包含视觉上很重要的大多数数据

如果用8-bit表示，则分割成8张位图

位图切割目的是提取关键信息

直方图处理：

直方图：$h(r_k)=n_k$

其中，$r_k\in [0,L-1]$：灰度级；$n_k$：灰度级为$r_k$的像素个数

即，统计每个像素值（灰度级）在像素点出现的次数

归一化直方图：（L=256？）

$p_r(r_k)=\frac{n_k}{n},0\leq p_r\leq 1,r_k=0,1,…,L-1,\sum_{r_k=0}^{L-1}p_r(r_k)=1
$

其中 n 是像素个数，$p_r(r_k)$是原始图像灰度分布的概率密度函数。

如果将$r_k$归一化到[0,1]之间，则$r_k$可以看作区间[0,1]的随机变量。

当直方图均匀分布时，图像最清晰。

直方图处理：

假设原图的灰度值变量为r，变化后新图的灰度值变量为s，希望寻找一个灰度变换函数$T: s=T(r)$，使得概率密度函数$p_r(r)$变换成希望的概率密度函数$p_s(s)$

灰度变换函数$T(r)$应该满足：

(1) $T(r)$在区间[0,1]中单调递增且单值（对一个自变量只有一个因变量的取值，多值如椭圆、圆）

(2) $\forall r\in [0,1]$，有$T(r)\in [0,1]$

直方图是近似的概率密度函数，所以用离散灰度级进行变换时很少得到完全平坦的结果。

变换后灰度级减少，即出现灰度“简并”的现象，造成了灰度级层次的丢失。

直方图均衡化的缺陷：

不能用于交互方式的图像增强应用，因为只产生唯一一个结果。

直方图规定化：

将原始图像的直方图转换为期望的直方图的形状

利用均衡化原理

设 ${r_k}$ 是原图像的灰度级
${z_k}$ 是符合指定直方图结果图像的灰度级

目标：找到一个灰度变换函数：$z_k=T(r_k),r\rightarrow z$

算法思路：

$p_r(r)$：原图的灰度密度函数

$p_z(z)$：希望得到的灰度密度函数

分别对$p_r(r),p_z(z)$作直方图均衡化处理，有：

$s=T(r)=\int_0^r p_r(r)dr,r\in[0,1]$

$v=G(z)=\int_0^r p_z(z)dz,z\in[0,1]$

经过变换得到的灰度s和v，

直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。例如，过曝光图像的灰度级集中在高亮度范围内，而曝光不足将使图像灰度级集中在低亮度范围内。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布（均衡）的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。换言之，直方图均衡化的基本原理是：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。

对一幅灰度图像，其直方图反映了该图像中不同灰度级出现的统计情况。